Guardrail System: The True Definition of Post Spacing

Warning:
This blogpost is exclusively written for structural engineers. Non-engineers may find this blogpost unentertaining.

---

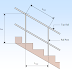
A TYPICAL GUARDRAIL SHOWN WITH TYPICAL LOADINGS

The post spacing, L, is generally defined simply as the horizontal distance between adjacent rail posts regardless of whether the rail is sloping or horizontally oriented.

Unfortunately, engineer's obscure understanding of the 50-lb/ft uniform railing load also obscures the definition of post spacing that turns it into an inclined distance between adjacent posts -- an obscure idea that this blogpost is trying to disprove.

The analysis and design of post for guardrail are quite simple. Being a flexural member, a guardrail post is normally idealized as a vertically-oriented cantilever beam, fixed at the bottom end and subjected to a concentrated load at the top free end.

The concentrated load at the top of a rail post originates from a single 200-lb concentrated load and a 50-lb/ft uniform load specified for a railing system by some building codes. The two loads, however, are not applied concurrently.

When the 200-lb concentrated load, P, is applied at the top of a rail post, a portion of the load is distributed to the adjacent posts on both sides through the horizontal rails -- thereby reducing the effective load on the rail post. This reduction is dependent on the stiffness of posts and the stiffness of horizontal rails that comprised the guardrail system. Generally, this type of loading does not directly define the rail post spacing.

When the 50-lb/ft uniform load, w, is applied at the top rail, the amount of load that a rail post sustains is dependent on the spacing between posts -- which translates into load tributary length. The wider the post spacing, the greater the load tributary length will be and, subsequently, the greater the load that a rail post sustains. Hence, this is the type of loading that determines and defines the post spacing. The maximum spacing that a rail post may attain is a function of its strength. Although the top rail may also control the spacing of rail post, this discussion only covers the rail post. Let us just assume here that the top rail is not the controlling guardrail member.

During my stint designing guardrail systems (or I may say just doing design calculations), I virtually established the logical definition of rail post spacing from my engineering point of view. It simply states that the true spacing of post is the horizontal distance between adjacent posts, regardless of whether the rail is sloping or horizontally oriented. Recognizing the correct definition is deemed necessary because correct interpretation of rail post spacing is paramount in the analysis of rail post -- as it is the basis for load calculation. Post spacing translates into load tributary length which means if an engineer held the wrong definition -- he has got the wrong load calculation and, subsequently, got the wrong design.

For quite a LONG time, I've been doing design calculations for railing with ease and without any adverse comments from the EORs. And for quite a long time, too, the idea that post spacing has to be taken as the horizontal distance between adjacent posts was never called into question. It has become, by default, an accepted norm in the analysis of railing. However, lately, I was dismayed to learn that an engineer from a consultancy firm that used to sign and seal our design calculations has questioned the 'norm'. Soon enough, in a form of calculation comment, he rejected our design calculations and argued that the load tributary length or post spacing shall be taken as the inclined distance between adjacent posts. The comment was not just a simple assertion of one's point of view but has become a directive to follow -- as this guy was never open to a discussion. It is more of an assertion of his authority over us.

We have made several attempts to further assert our idea on this simple engineering issue but, apparently, our efforts were rendered futile as the guy refused to budge on the issue. Well, where do you think we have to position ourselves on this issue against an engineering authority? Nowhere -- but to self-suppress our own ideas against our own will. Why? Because the threat is there: they won't be 'signing and sealing' our calculations if we continue to argue with them on this issue. And to add more insult to the injury, our higher-ups, sensing that we could not win a debate against an engineering authority, succumb to the threat. Otherwise, they will be obliged to look for another consultancy firm, that share the same idea with us, to sign and seal our design calculations -- entailing a waste of time and money.

As a consequence, we are now designing a railing system based on the approach authoritatively laid down on us, which we deem as an upshot of an obscure idea. The 'directive' was to apply the 50-lb/ft uniform load along the inclined length of rail, which corresponds to the inclined distance between posts. Somewhat defiant, we regard such an idea as an 'engineering fallacy', a hasty generalization. Why? Because we thought that this guy didn't even bother to explore what really generates the 50-lb/ft uniform load on the rail, the nature of the load and how it behaves when applied to the railing.

For example, how do you treat a 12-ft handrail, inclined at an angle approaching 90 degrees, to receive the 50-lb/ft uniform loading? Do you think a handrail with such almost-vertical inclination will still be able to accommodate people to facilitate climbing? The answer, of course, is NO. Now, would you agree that at such inclination the handrail is accommodating a load of 650 lbs -- the product of 50-lb/ft and the 12-ft length of handrail? The answer, of course, is still NO. Why? This is because the group of persons that generates the 50-lb/ft uniform load remains standing upright and does not align itself perpendicular to the inclined handrail. During a stair climb, each individual in the group changes its vertical position along the stair, but the group does not change their density nor the intensity of their push on the railing. Clearly, this suggests that the 50-lb/ft uniform load does not necessarily apply linearly along the inclined length of the handrail.

So, why do engineers differ in interpretations when it comes to how the 50-lb/ft uniform load be applied to the handrails? The main reason -- most building codes did not provide a clear definition of the load; they only mention the numeric description of the load. This is where the gray area lies -- the cause of confusion. I read one building code, and it merely states that 'handrails be designed to resist a load of 50-lb/ft' but did not discuss what the load is all about. With the absence of description, an engineer's tendency is to numerically generalize the load. And the most convenient way for an engineer to do is to multiply the load by the length of the rail, presto, to obtain the load sustained by the rail posts without taking into account what actually generates the load or where does the load come from.

The bottom line, there must be a logic hidden somewhere regarding the application of the 50-lb/ft uniform load to the railing system. And for certain, the idea of applying the 50-lb/ft uniform load along the inclined length of the rail (suggested by that consultancy engineer) is absolutely a blunder in engineering analysis. The 50-lb/ft uniform load should be applied along the horizontal length of the rail. This is what actually this blog post attempts to prove here.

The 50 lb/ft Load According to IBC

---

According to INTERNATIONAL BUILDING CODE (IBC), "Handrails and guards shall be designed to resist a load of 50-lb/ft applied in any direction at the top and to transfer this load through the supports to the structure." [See IBC 2009, section 1607.7.1]

There seems to be a problem in the sentence in the above paragraph. The phrase 'in any direction' used by IBC is vague and is subject to several interpretations. With respect to the analysis of rail, the phrase 'in any direction' could mean a side-ward push, a downward push, an upward pull or even a pull along the length of the rail -- depending on the engineer's interpretation. Adding to the confusion is IBC's failure to define the origin of the load and what the load represents.

As a consequence, there exist several conflicting ideas, most particularly in the analysis of rail post -- leading to different design results. Had the 50 lb/ft load been defined as wind load, then the phrase 'in any direction' would have been in perfect conformance with the perceived load condition, since wind may blow from almost all directions.

On the other hand, had the load been defined as a live load generated by humans, then the phrase 'in any direction' could, at least, be interpreted in two possible ways: it could either be a downward or a side-ward push on the handrail.

The 50 lb/ft Load According to ANSI/NAAMM (AMP 521-01)

---

Fortunately, on page 14 of PIPE RAILING SYSTEM MANUAL, 4th Edition (AMP 521-01) published by National Association of Architectural Metal Manufacturers (NAAMM), a written definition of the load can be found. According to NAAMM, "Uniform loading, specified by some building codes, represents the force exerted by tightly grouped persons leaning on or pressing against the railing system."

So, there it goes. With the use of the phrases, leaning on and pressing against, it is now very clear that the 50 lb/ft uniform load specified by IBC is -- a side-ward push (or a downward push) exerted by tightly grouped persons to the railing system.

Let us put in mind that NAAMM's definition of the load does not contradict IBC, but supplements what has been lacking on IBC's description of the 50 lb/ft load.

The Human Body Under the Influence of Gravity

---

A MECHANICAL GYROSCOPE

Gyroscopic Effect: The orientation of the rotating yellow disk at the center is unaffected by the rotation of the three gimbals about their respective axes of rotation.

Understanding how the human body behaves under the influence of gravity may help clear up confusion on engineer's understanding of tributary length for the loading of rail post.

We may not be mindful of how we are influenced by gravity in our day-to-day activities, but the tendency of our bodies regardless of where we stand on the surface of the planet we called earth, whether on a flat or inclined surface -- is to remain aligned with the direction of gravity. In other words, whether we like it or not, our bodies will always be vertically oriented, no matter how steep the slope of the surface we are standing on.

Proof? Try climbing or walking on a stair or ramp, and you will find out that no matter what you do, your body will remain upright or vertically oriented and will never align perpendicular to the stair's inclination. This is because a human body has a built-in natural GYROSCOPE that does the trick to keep it aligned with the direction of gravity.

Our body's built-in GYROSCOPE is our vestibular system, which provides us our sense of balance and spatial orientation. Our vestibular system is an inertial sensor that works to coordinate our movement with balance in relation to our environment. Gravity is one of the environmental aspects that our vestibular system monitors and senses. While in motion, our vestibular system detects even a slight shift in our body's center of gravity and performs compensatory movements and adjustments in our body position. This is the reason why, in an unconscious effort, we always remain upright regardless of the condition of the surface we are standing on -- such as a sloping stair.

Effect of Body's Alignment to Gravity on Posts Spacing and Tributary Load of Post

---

A 'TIGHTLY GROUPED PERSONS'

---

Figure 1: HORIZONTAL POSITION

---

Figure 2: CLIMBING POSITION

The number (density, to be exact) of persons initially on the horizontal surface is the same number of persons that covers the sloping stair in climbing position; hence, the total side-ward push on the rail remains the same. This proves that the total push is a function of the horizontal distance, and NOT the INCLINED distance covered by the tightly grouped persons.

---

Figure 3: THE ANTIGRAVITY LEAN

Kill me if I am wrong! Nobody on this planet can lean backward or forward (except the late Michael Jackson, who used a contraption known as the antigravity shoes to do the trick) and align himself perpendicular to the sloping stair during a stair climb. Hence, a tightly grouped persons cover the horizontal distance, L, in the upright position -- and not the inclined elongated distance of the stair in leaning position.

This suggests that the 50-lb/ft uniform load is a global loading that always applies parallel to the horizontal plane or to the earth's surface. It is, therefore, an engineering blunder to argue that the 50-lb/ft be applied along the length of the sloping rail.

Let us assume that a tightly grouped persons are being represented by individuals falling in a straight line as shown. Each individual row in the group is numerically labeled in sequence from 1 to 12 to represent density. Also, let us assume that the group covers a distance, L, from start to end. Further, let us assume that the group transitions from a horizontal position (Figure 1) to the climbing position (Figure 2).

Due to the inherent gyroscopic ability of a human body to align itself with the direction of gravity, a tightly grouped persons (Figure 1) on horizontal position will still occupy the same LENGTH OF COVERAGE, L, (Figure 2) while on climbing position and, therefore, exerts the same magnitude of side-ward push onto the rail posts. Based on this premise, taking into account the 50-lb/ft uniform load, we can conclude that the lateral push exerted by a tightly grouped person is clearly a function of the horizontal coverage distance L and absolutely not a function of the inclined distance of the stair or rail. The horizontal coverage distance L represents either the spacing of post or the load tributary length of post.

Such is true because the very manner in which the tightly grouped persons moved up and fit into the sloping stair (Figure 2) is a simple case of elevating each and every individual body in the group while maintaining its individual position along the horizontal axis. Logically, this effect is analogous to shearing or sliding a deck of cards where the deck of cards appears to be diagonally lengthened, but the number of cards remains the same.

In contrast, there is absolutely no way a tightly grouped persons can climb a sloping surface in antigravity leaning position, as shown in Figure 3. Those who argued and proposed that the 50-lb/ft uniform load be applied along the inclined length of the rail or stair -- might need hundreds of individuals with the likes of Michael Jackson, who has an apparent ability to do an antigravity lean, to fill the whole stretch of the stair in leaning position.

Just like the sheared deck of cards, the density or the number of individuals in a tightly grouped persons is unchanged when it climbs a sloping surface or a stair. Once more, this further confirms that the number of persons initially on the horizontal surface (Figure 1) is the same number of persons that will cover a sloping surface or a stair in climbing position (Figure 2). This provides us the premise necessary to establish the following facts:

• The lateral or side-ward push exerted by a tightly grouped persons on the railing system remains the same regardless of whether the stair or rail is sloping or horizontally oriented. The human body's tendency to align itself with the direction of gravity turns the 50-lb/ft uniform load into a global load.

• Subsequently, when calculating the tributary load at the top of rail post due to the 50-lb/ft uniform lateral or side-ward push exerted by a tightly grouped persons, the load tributary length shall be taken as the horizontal distance between adjacent posts as very clearly proven by Figure 1 and Figure 2.

• The true definition of 'spacing of railing post' is simply THE HORIZONTAL DISTANCE BETWEEN ADJACENT POSTS regardless of whether the railing is sloping or horizontally oriented -- and, absolutely, it is NOT the INCLINED distance between adjacent posts as proposed by that engineer from a consultancy firm.

Mathematical Proof: Inclined Distance as Tributary Length or Spacing - An Engineering Blunder

---

The true Load Tributary Length and Post Spacing. Is it the Horizontal Distance or the Inclined Distance?

When tightly grouped persons are placed to stand on an inclined stair (see Figure 2), like shearing or sliding a deck of cards, they only shift their individual elevation to fit into the stair but maintain their number -- thus, exerting a push onto the post as if they are on the horizontal position (see Figure 2).

Consider a guardrail with uniformly spaced posts along its length. Assume that the railing, along with the stair, has a slope of 3:4 as shown. Also, assume the uniform post spacing of the railing is 4 feet along the horizontal. With the given slope of 3:4 and a horizontal distance of 4 feet, we got a perfect right triangle with side dimensions of 3 feet, 4 feet, and 5 feet.

Isolating the numbers for calculation convenience, we got the following:

• The uniform distance L (4'-0") represents the horizontal spacing of rail post. The distance also represents the tributary length covered by a tightly grouped persons on horizontal position (Figure 1) attributed to each rail post.

• The uniform distance D (5'-0") represents the inclined distance between rail posts. According to some engineers, that consultancy engineer, in particular, this is the distance that the 50-lb/ft is supposed to be linearly applied. This is the same distance that they used to claim as the spacing and load tributary length attributed to a single post.

Now, considering the 50-lb/ft uniform push exerted by tightly grouped persons onto the guardrail, let us calculate the force sustained by a rail post from both engineering perspectives -- from one that considers the horizontal distance as the post spacing and from the other that considers the inclined distance as the post spacing. Numerically, the result will prove that either one of these perspectives is an engineering blunder.

According to that brilliant engineer of a consultancy firm who rejected our design calculations, the load tributary length attributed to a rail post shall be taken as the inclined distance between posts. Based on the above illustration, he is apparently referring to the inclined distance D (5'-0"). Granting that he is correct, then the total push exerted by a tightly grouped persons on a post is the product of the 50-lb/ft uniform load and the inclined distance 'D' -- which is equal to 250 pounds. But, is he really correct? I don't really think so.

Actually, he is not correct. Or, to be exact, he is very much wrong. Why? The reason is that his perspective has an apparent gray area. For example, from the figure above, if we increase the angle of inclination of the stair and handrail while maintaining the same distance L, the inclined length of the rail also increases. Similarly, if we decrease the angle of inclination of the stair and handrail, the inclined length of the rail also decreases. This suggests, based on his perspective, that the load or push on a post changes as the angle of inclination changes. How is this possible? Isn't it that when a tightly grouped persons are placed to stand on an inclined stair -- they only shift their individual elevation to fit into the stair but maintain their number? So, why is there a change in horizontal push to a post in the first place? Does that mean that if a single individual traverses an inclined stair, he is multiplying himself to account for the supposed increase in push on the post?

Here is the fact: The number of individuals in a tightly grouped persons remains the same when the group transitions from horizontal position into climbing position. The tightly grouped persons, elaborating the word tight, is incompressible; so that in a climbing position, each individual in the group only shifted their individual elevation to fit into the stair but still covers the same horizontal distance. This means that the number of people that climbed the stair is the same number of people that is originally on the horizontal position. Thus, the total push on a post should be the product of the 50-lb/ft uniform push and the horizontal distance L. It must be equal to 200 pounds, not 250 pounds.

Therefore, the idea proposed by some engineers (that consultancy engineer to be specific) that rail post spacing or load tributary length for rail post shall be taken as the inclined distance between adjacent rail posts -- is an absolute engineering analysis blunder.